Evaluating the Transfer of Information in Phase Retrieval STEM Techniques

Julie Marie Bekkevold; Stephanie M Ribet; Mary C Scott; Lewys Jones; Colin Ophus; Georgios Varnavides

doi:10.69761/ehch7395

Computational Article

Contents

While traditionally, direct ptychography techniques have utilized pixelated detectors, the methods generalize well to segmented detectors Yang et al., 2015. This allows us to leverage the benefits outlined in the previous section, including faster dwell times for increased temporal resolution Bekkevold et al., 2024.

Analytical Segmented SSB CTF¶

The segmented SSB CTF can be derived analytically by binning the aperture-overlap function using the detector geometry, prior to taking its absolute value:

\mathcal{L}^{\mathrm{S-SSB}}(\bm{q}) = \frac{\mathrm{i}}{2} \sum_j \int \left| D_j (\bm{k}) \Gamma(\bm{q},\bm{k}) \right|d\, \bm{k} .

(9.1)

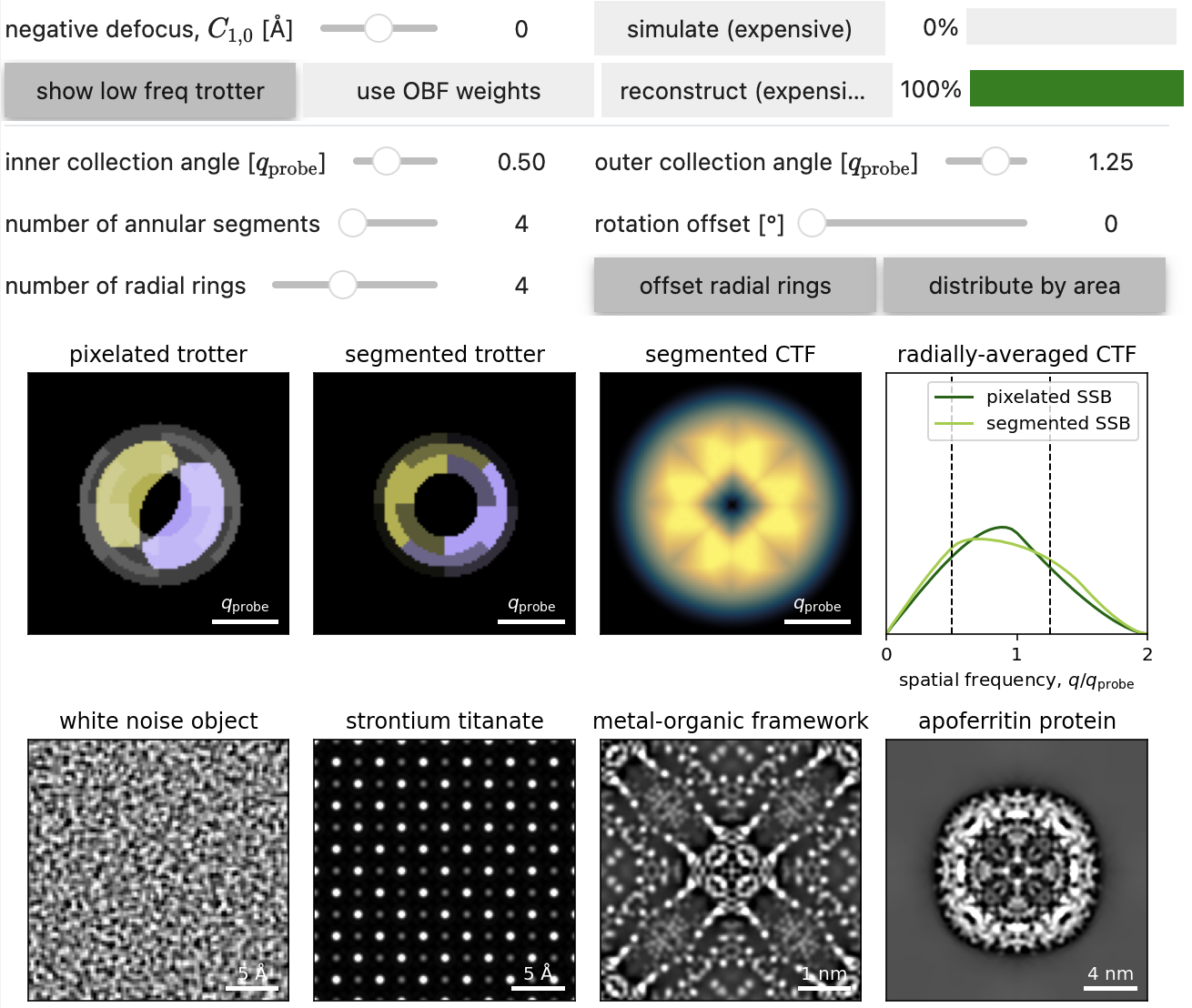
Figure 9.1 plots the SSB CTF for various detector geometries, highlighting how the symmetry of the detector is reflected in the symmetry of the two-dimensional CTF.

Effect of detector geometries on the CTF for SSB direct ptychography.
The double-triple overlap regions are colloquially referred to as “trotters”, due to their visual similarity with a . — Figure 9.1:Effect of detector geometries on the CTF for SSB direct ptychography. The double-triple overlap regions are colloquially referred to as “trotters”, due to their visual similarity with a Pig's trotter.

We note the following:

As the number of radial and annular segments is increased, the aperture-overlap function or “trotters” are better sampled, yielding a more accurate CTF.
- This is particularly important when the probe includes aberrations, as the aperture-overlap function is no longer uniform in phase.
The detector geometry results in a highly anisotropic 2D CTF, with the CTF approaching zero near the edges of each segment.
- Note this effect is obfuscated in the radially averaged 1D CTF.

Noise Optimizing OBF Weights¶

Optimum Bright Field (OBF) STEM bears many similarities with phase-compensated SSB, and was in-fact developed specifically to optimize the signal-to-noise ratio in reconstructions using segmented detectors Ooe et al., 2021Ooe et al., 2024.

This is done by using a different normalization than SSB in phase-compensating the measured aperture-overlap function, given by:

\begin{aligned} \mathcal{L}^{\mathrm{S-OBF}}(\bm{q}) &= \frac{\mathrm{i}}{2} \sum_j \int D_j (\bm{k}) A(\bm{k}) K(\bm{q}) d\, \bm{k} \\ K(\bm{q}) &= \left( \int \frac{\left| D_j (\bm{k}^{\prime}) \Gamma(\bm{q},\bm{k}^{\prime}) \right|^2} {D_j (\bm{k}^{\prime}) A(\bm{k}^{\prime})} d\, \bm{k}^{\prime} \right)^{-1/2}, \end{aligned}

(9.2)

where $A(\bm{k})$ is the normalized probe aperture.

Note that using the OBF weights in Figure 9.1 above, results in broadening the SSB CTF, and minimizing the anisotropic influence of detector segmentation on the 2D CTF.

References¶

Yang, H., Pennycook, T. J., & Nellist, P. D. (2015). Efficient phase contrast imaging in STEM using a pixelated detector. Part II: Optimisation of imaging conditions. Ultramicroscopy, 151, 232–239. 10.1016/j.ultramic.2014.10.013
Bekkevold, J. M., Peters, J. J. P., Ishikawa, R., Shibata, N., & Jones, L. (2024). Ultra-fast Digital DPC Yielding High Spatio-temporal Resolution for Low-Dose Phase Characterization. Microscopy and Microanalysis, 30(5), 878–888. 10.1093/mam/ozae082
Ooe, K., Seki, T., Ikuhara, Y., & Shibata, N. (2021). Ultra-high contrast STEM imaging for segmented/pixelated detectors by maximizing the signal-to-noise ratio. Ultramicroscopy, 220, 113133. 10.1016/j.ultramic.2020.113133
Ooe, K., Seki, T., Nogami, M., Ikuhara, Y., & Shibata, N. (2024). Dose-efficient phase-contrast imaging of thick weak phase objects via OBF STEM using a pixelated detector. Microscopy, 74(2), 98–106. 10.1093/jmicro/dfae051

Segmented Detector CTF

Segmented iCOM

Segmented Detector CTF

Segmented tcBF

[cite-yang_efficient_2015] Yang, H., Pennycook, T. J., & Nellist, P. D. (2015). Efficient phase contrast imaging in STEM using a pixelated detector. Part II: Optimisation of imaging conditions. Ultramicroscopy, 151, 232–239. 10.1016/j.ultramic.2014.10.013

[cite-bekkevold_ultra-fast_2024] Bekkevold, J. M., Peters, J. J. P., Ishikawa, R., Shibata, N., & Jones, L. (2024). Ultra-fast Digital DPC Yielding High Spatio-temporal Resolution for Low-Dose Phase Characterization. Microscopy and Microanalysis, 30(5), 878–888. 10.1093/mam/ozae082

[cite-Ooe_2021] Ooe, K., Seki, T., Ikuhara, Y., & Shibata, N. (2021). Ultra-high contrast STEM imaging for segmented/pixelated detectors by maximizing the signal-to-noise ratio. Ultramicroscopy, 220, 113133. 10.1016/j.ultramic.2020.113133

[cite-Ooe_2024] Ooe, K., Seki, T., Nogami, M., Ikuhara, Y., & Shibata, N. (2024). Dose-efficient phase-contrast imaging of thick weak phase objects via OBF STEM using a pixelated detector. Microscopy, 74(2), 98–106. 10.1093/jmicro/dfae051

Direct Ptychography with a Segmented Detector

Analytical Segmented SSB CTF¶

Noise Optimizing OBF Weights¶