Evaluating the Transfer of Information in Phase Retrieval STEM Techniques

Julie Marie Bekkevold; Stephanie M Ribet; Mary C Scott; Lewys Jones; Colin Ophus; Georgios Varnavides

doi:10.69761/ehch7395

Computational Article

Contents

So far, this article has focused on deriving analytical and numerical CTFs for various reconstruction techniques and experimental parameters, notably probe aberrations and segmented detector geometry. The CTF is an important metric in evaluating linear imaging systems, representing the maximum usable signal. However, it fails to capture the Poisson-limited nature of physical detectors for experiments done with finite electron fluence.

Spectral Signal to Noise Ratio¶

To remedy this, we utilize a statistical framework to evaluate the transfer of information of the various reconstruction techniques and acquisition parameters. Specifically, we perform independent reconstructions on simulated diffraction intensities with finite electron fluence by performing $M$ Poisson draws on the same white noise object. We then analyze the reconstruction fidelity using the spectral signal-to-noise ratio (SSNR) defined as Unser et al., 1987:

\begin{aligned} \mathrm{SSNR}(\bm{q}) &= \frac{\left| \sum_i \Phi_i(\bm{q}) / M \right|}{ \sqrt{ \sum_i \left| \Phi_i(\bm{q}) - \bar{\Phi}(\bm{q}) \right| / (M-1)} } \\ \Phi_i(\bm{q}) &= \mathcal{F}_{\bm{r} \rightarrow \bm{q}}\left[\phi_i^{\prime}(\bm{r}) \right], \end{aligned}

(13.1)

where the overbar denotes an average value. Intuitively, (13.1) represents the absolute value of the sample mean divided by the sample standard deviation of the independent reconstructions for each spatial frequency $\bm{q}$ .

Detective Quantum Efficiency¶

We note in passing that the simple SSNR metric defined in (13.1), is closely related to detective quantum efficiency (DQE) – another popular metric in analyzing the efficiency of linear imaging systems – according to Bennemann et al., 2024:

\mathrm{DQE}(\bm{q}) = \frac{\mathrm{SSNR}_{\mathrm{out}}^2(\bm{q})}{\mathrm{SSNR}_{\mathrm{in}}^2(\bm{q})},

(13.2)

where $\mathrm{SSNR}_{\mathrm{in}}(\bm{q})$ denotes the SSNR of a reference or “ideal” reconstruction. This is usually taken as the HRTEM SSNR when using an ideal Zernike phase-plate Zernike, 1942, which for a white-noise object is simply given by the squared root of the electron fluence. As such, the metrics are trivially related in our case, and in what follows we use the simpler SSNR metric.

iCOM SSNR¶

Figure 13.1 plots the SSNR calculation for in-focus pixelated and segmented iCOM, using $M=256$ and a total electron budget of $N_e = 10^8 \, e^-/\mathrm{probe}$ . We note the following:

The SSNR numerator, which corresponds to the maximum usable signal, is identical to the absolute value of the CTF we computed in Integrated Center of Mass Imaging with a Pixelated Detector and Integrated Center of Mass Imaging with a Segmented Detector.
The iCOM reconstruction noise, given by the SSNR numerator, is inversely proportional to the spatial frequency, $\bm{q}$ .
- As such, the SSNR metric correctly tends to zero for both $\bm{q}\rightarrow 0$ and $\bm{q} \rightarrow 2\, q_{\mathrm{probe}}$
In contrast to the segmented detector signal, the segmented detector noise exhibits no dependence on the detector geometry.
- The same is true for the effect of probe aberrations.

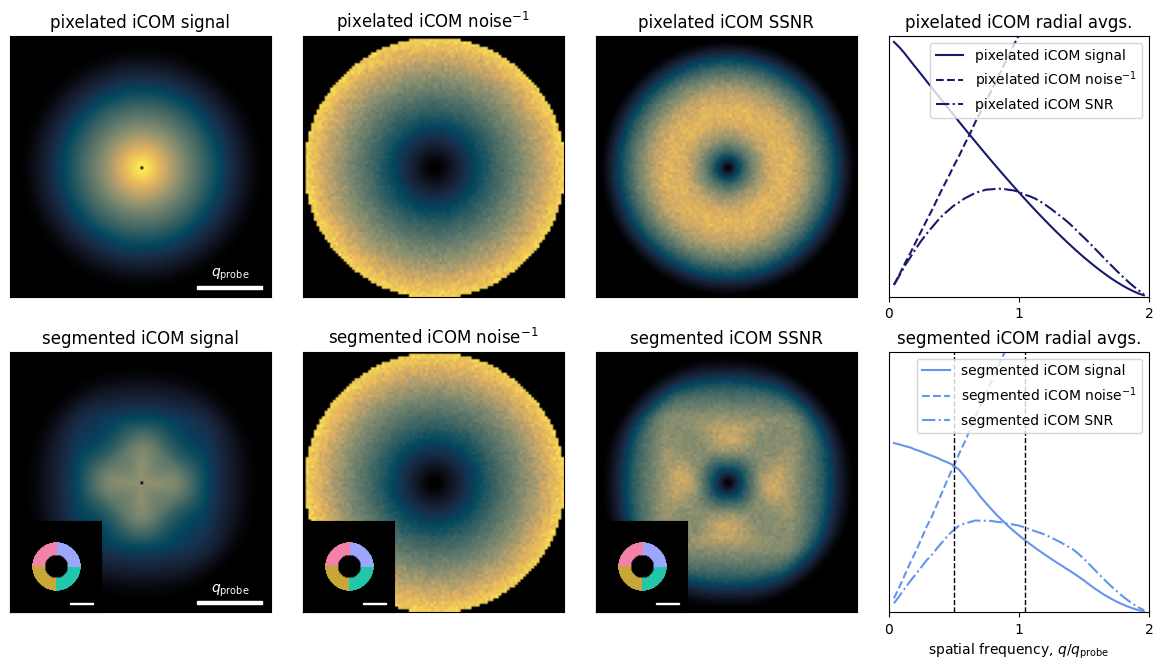
Figure 13.1:SSNR calculation for pixelated and segmented iCOM, highlighting that the noise is inversely linear with spatial frequency and is independent of detector geometry.

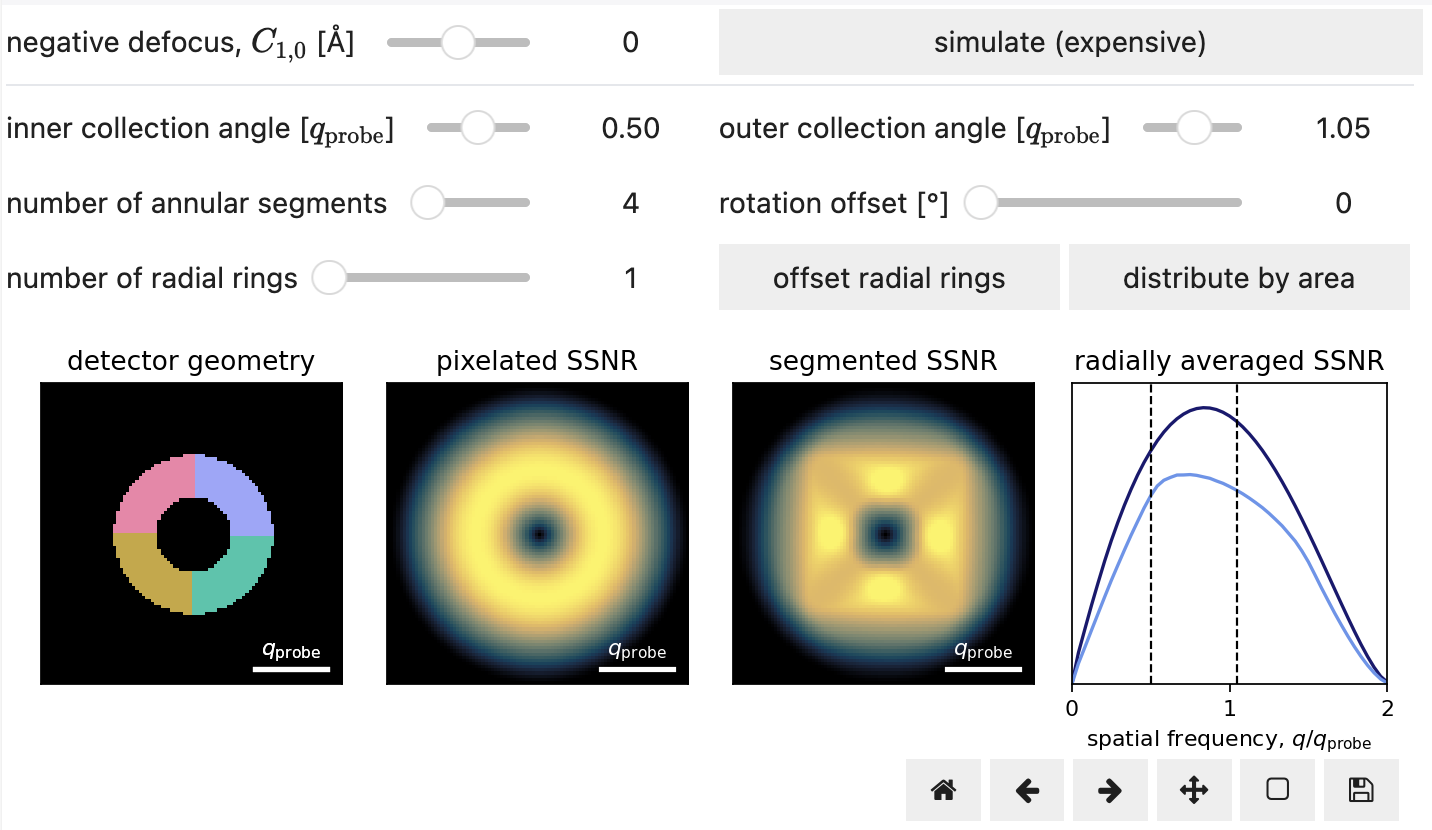
This last observation suggests we can use an analytical expression for the iCOM noise as $\bm{q}^{-1}$ , and thus compute the iCOM SSNR faster. Figure 13.2 illustrates this interactively, allowing practitioners to quickly evaluate the iCOM SSNR for various detector geometries and acquisition parameters.

Figure 13.2:Interactive widget demonstrating analytical iCOM SSNR for various detector geometries.

References¶

Unser, M., Trus, B. L., & Steven, A. C. (1987). A new resolution criterion based on spectral signal-to-noise ratios. Ultramicroscopy, 23(1), 39–51. 10.1016/0304-3991(87)90225-7
Bennemann, F., Nellist, P., & Kirkland, A. (2024). Quantitative comparison of HRTEM and electron ptychography. BIO Web of Conferences, 129, 04007. 10.1051/bioconf/202412904007
Zernike, F. (1942). Phase contrast, a new method for the microscopic observation of transparent objects part II. Physica, 9(10), 974–986. 10.1016/s0031-8914(42)80079-8

Segmented Detector CTF

Upsampled Direct Ptychography

Segmented Detector CTF

Conclusions

[cite-Unser_1987] Unser, M., Trus, B. L., & Steven, A. C. (1987). A new resolution criterion based on spectral signal-to-noise ratios. Ultramicroscopy, 23(1), 39–51. 10.1016/0304-3991(87)90225-7

[cite-Bennemann_2024] Bennemann, F., Nellist, P., & Kirkland, A. (2024). Quantitative comparison of HRTEM and electron ptychography. BIO Web of Conferences, 129, 04007. 10.1051/bioconf/202412904007

[cite-Zernike_1942] Zernike, F. (1942). Phase contrast, a new method for the microscopic observation of transparent objects part II. Physica, 9(10), 974–986. 10.1016/s0031-8914(42)80079-8