Evaluating the Transfer of Information in Phase Retrieval STEM Techniques

Julie Marie Bekkevold; Stephanie M Ribet; Mary C Scott; Lewys Jones; Colin Ophus; Georgios Varnavides

doi:10.69761/ehch7395

Computational Article

Contents

One of the main advantages of tcBF, is that the achievable resolution is set by the numerical aperture and the accuracy to which the lateral shifts in the vBF images can be measured to. Since these lateral shifts are often measured with sub-pixel precision, the tcBF technique is not scan-sampling limited and instead the aligned vBF images can be “upsampled” to produce high-resolution, coherent vBF images. This significantly relaxes sampling constraints, which in-turn reduces the effects of drift and allows for better dose management.

However, as we saw in Figure 5.1, the tcBF CTF exhibits notable zero-crossings which limit the usable information at certain frequencies and necessitate the need for “phase-flipping” corrections to avoid contrast reversals. By contrast, direct ptychography techniques, exhibit a purely positive CTF with similar oscillations due to the aberration surface, but to date have been scan-sampling limited.

SSB split operator decomposition¶

The aperture overlap function factorization we derived in (5.2), $\Gamma(\bm{q},\bm{k}) \approx \Beta(\bm{q},\bm{k}) \mathrm{e}^{\mathrm{i\nabla_{\chi}\cdot\bm{k}}}$ , suggests that the SSB phase-correction operator can be split into two parts (see Algorithm 12.1):

Phase-correction for the effect of shifted apertures, using the $\Beta(\bm{q},\bm{k})$ kernel
Sub-pixel shifting for the observed lateral vBF shifts, using the $\mathrm{e}^{\mathrm{i\nabla_{\chi}\cdot\bm{k}}}$ phase ramp,

recovering the SSB CTF, using sub-sampled acquisitions.

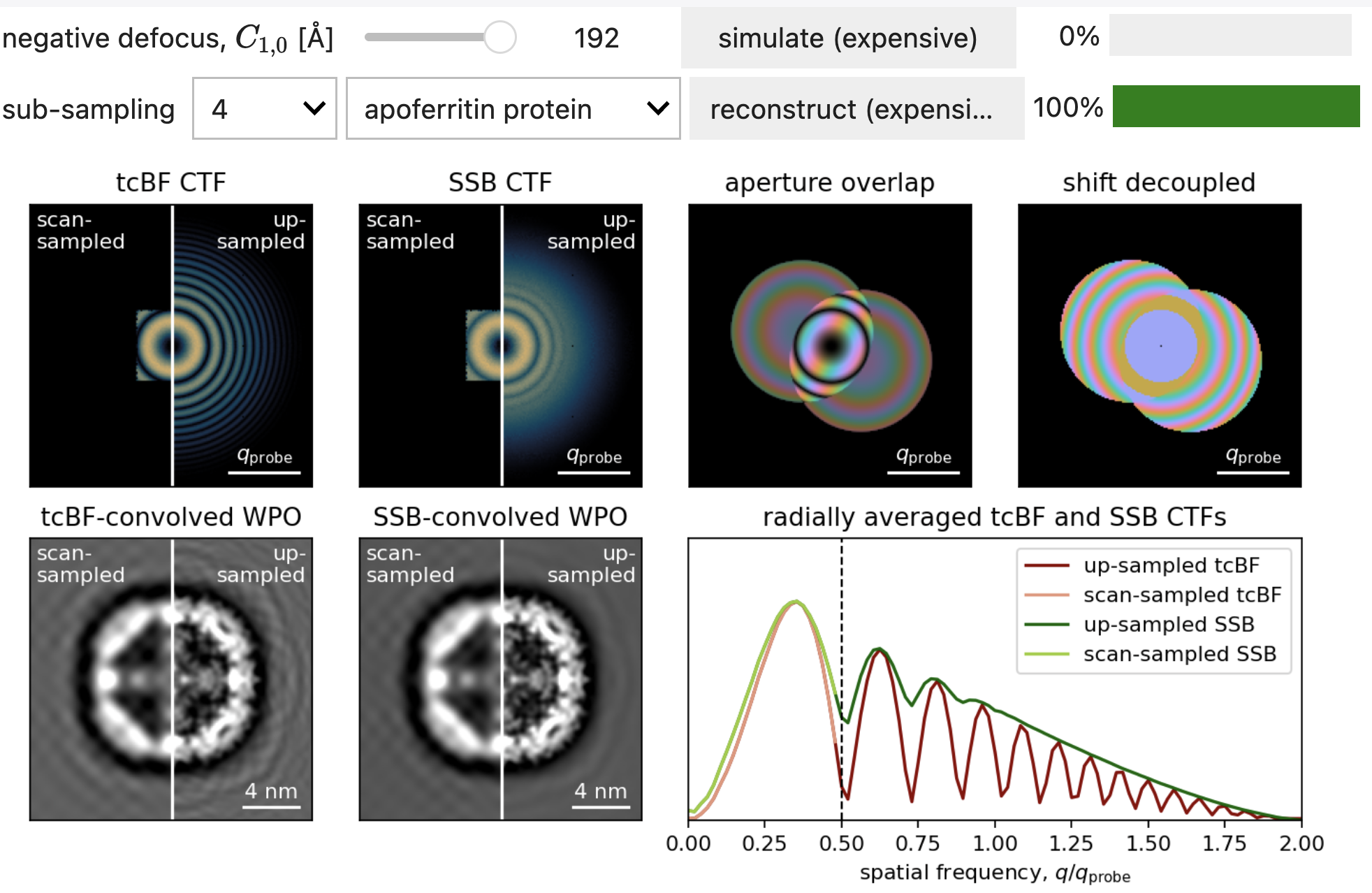
Figure 12.1:SSB split-operator decomposition, illustrating sub-sampling capabilities.

Figure 12.1 demonstrates this technique interactively for various defocus and sub-sampling values. We note the following:

The upsampled tcBF and SSB CTFs match the Nyquist-sampled CTFs we derived in Tilt-Corrected Bright-Field STEM with a Pixelated Detector and Direct Ptychography with a Pixelated Detector.
Convolving the SSB CTF with a WPO result in significantly improved reconstructions over convolving with the tcBF CTF, due to the lack of zero-crossings.
Larger defocus values are more robust to higher sub-sampling factors, since the measured lateral-shifts, and thus the phase-ramp shifts, are larger than the scan sampling.
- In the limit of no defocus, the upsampled SSB CTF becomes very noisy.

Upsampled SSB pseudocode

Algorithm 12.1 (Upsampled SSB reconstruction)

Output: Reconstructed single-sideband image $\tilde{I}(\bm{r})$ , upsampled to Nyquist sampling
Data: sub-sampled 4D-STEM dataset, $I(\bm{r},\bm{k})$
Inputs:

Convergence semiangle, $k_0$
Set of aberration coefficients, $C_{m,n}$ (e.g. negative defocus, $C_{1,0}$ )

Initialization:

Define set of BF indices of size $N_{\mathrm{BF}}$
$K_{\mathrm{BF}} = \left\{\bm{k} : \| \bm{k} \| \lt k_0 \right\}$
Define normalized top-hat aperture function,
$A(\bm{k}) = \begin{cases} 1/N_{\mathrm{BF}} & \mathrm{if} \quad \bm{k} \in K_{\mathrm{BF}} \\ 0 & \mathrm{otherwise} \end{cases}$
Compute aberration surface and gradients (e.g. using only $C_{1,0}$ ):
$\chi(\bm{k}) = \pi \lambda C_{1,0} \|\bm{k}\|^2, \quad \nabla_{\chi}(\bm{k}) = 2 \pi \lambda C_{1,0} \bm{k}$
Sample aberration surface gradients at BF indices $K_{\mathrm{BF}}$ to obtain set of shift vectors:
$\Delta \bm{k}_{\mathrm{BF}} = \left\{\nabla_{\chi}(\bm{k}) : \bm{k} \in K_{\mathrm{BF}} \right\}$
Define set of virtual BF images of size $N_{\mathrm{BF}}$
$I_{\mathrm{BF}} = \left\{ I(\bm{r},\bm{k}) : \bm{k} \in K_{\mathrm{BF}} \right\}$
Initialize output image $\tilde{I}(\bm{r}) \leftarrow 0$

For each BF index $i = 1$ to $N_{\mathrm{BF}}$ Do:

$G \leftarrow \mathcal{F}_{\bm{r}\rightarrow\bm{q}}[I_{\mathrm{BF}}[i]]$
$G^{\prime} \leftarrow \mathit{tile}(G)$ to upsampled grid $\bm{k}$
Construct shift operator:
$\Delta \leftarrow \exp\left(\mathrm{i} \bm{k} \cdot \Delta \bm{k}[i]\right)$
Compute aperture overlap factor:
$\Beta \leftarrow e^{-i\chi(\bm{k})} A(\bm{k} - K_{\mathrm{BF}}[i]) - e^{i\chi (\bm{k})} A(\bm{k} + K_{\mathrm{BF}}[i])$
Update reconstruction:
$\tilde{I} \mathrel{+}= \mathrm{Im}\left(\mathcal{F}^{-1}_{\bm{k} \rightarrow \bm{r}}\left[\frac{G^{\prime} \, \Beta^{\ast} \, \Delta}{\left|\Beta\right|}\right]\right)/N_{\mathrm{BF}}$

End For (BF pixels)

We note the following:

The algorithm runtime is constant, since the loop is over the BF pixels and not over scan frequencies (as is usual in SSB).
- This implies that Nyquist-sampled SSB can also be sped up using the algorithm above, provided that $N_{\mathrm{BF}}$ is less than the number of scan pixels.
The above implementation uses tiled Fourier shifting, but the same decomposition can be achieved using e.g. kernel-density estimation (KDE) upsampling.

Segmented Detector CTF

Segmented iterative ptycho

Segmented Detector CTF

Spectral Signal to Noise

Upsampled Direct Ptychography

SSB split operator decomposition¶