Curvenote
Computational Article

Evaluating the Transfer of Information in Phase Retrieval STEM Techniques

https://doi.org/10.69761/ehch7395
Contents

Integrated Center of Mass Imaging with a Segmented Detector

One of the simplest ways to use the signal from a classical four-segmented detector is estimating the COM of the BF disk by subtracting opposing detector segments. It was shown over a decade ago that this enables imaging of single atomic columns Shibata et al., 2012. However, segmented detectors of other geometries may be realized as well, and the CTF framework lends itself well to investigating the information transfer dependency on the detector geometry.

Analytical Segmented COM CTF

In Integrated Center of Mass Imaging with a Pixelated Detector, we saw that the analytical CTF for iCOM with a pixelated detector is the autocorrelation of the complex probe, since the pixelated detector function Dj(k)=δ(k)D_j(\bm{k}) =\delta(\bm{k}) covers every pixel in the detector as seen in (3.3). For a segmented detector given by (7.1) the combined vectorial detector function is given by:

D(k)=∑jkx(k)Dj(k)k^x+∑jky(k)Dj(k)k^y,\bm{D}(\bm{k}) = \sum_j k_x(\bm{k})D_j(\bm{k}) \hat{k}_x + \sum_j k_y(\bm{k})D_j(\bm{k}) \hat{k}_y,
(8.1)

with the analytical segmented COM CTFs obtained by Lazić & Bosch, 2017:

LxS−COM(q)=[ψ⋆ψ Dx](q)−[ψ Dx⋆ψ](q)LyS−COM(q)=[ψ⋆ψ Dy](q)−[ψ Dy⋆ψ](q)\begin{aligned} \mathcal{L}^{\mathrm{S-COM}}_x(\bm{q}) &= \left[\psi \star \psi \, D_x \right](\bm{q}) - \left[\psi \, D_x \star \psi \right](\bm{q}) \\ \mathcal{L}^{\mathrm{S-COM}}_y(\bm{q}) &= \left[\psi \star \psi \, D_y \right](\bm{q}) - \left[\psi \, D_y \star \psi \right](\bm{q}) \end{aligned}
(8.2)

Detector Segmentation iCOM CTF

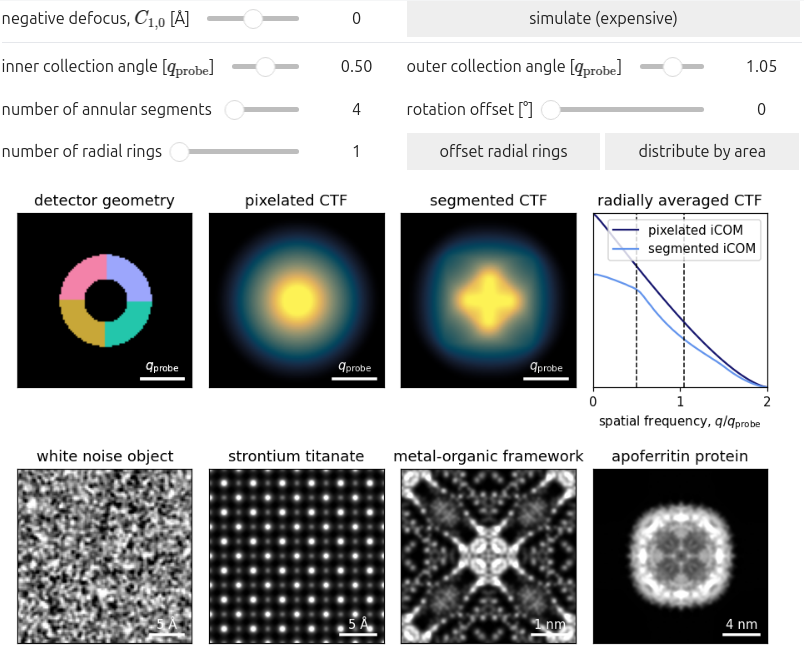
The iCOM CTF is then obtained from (8.2) using the same Fourier-integration technique given by (3.5). Figure 8.1 plots the iCOM CTF for various detector geometries, highlighting how the symmetry of the detector is reflected in the symmetry of the two-dimensional CTF.

Source:Segmented iCOM
Effect of various detector geometries on the CTF for iCOM imaging.

Figure 8.1:Effect of various detector geometries on the CTF for iCOM imaging.

We note the following:

  • As the number of annular and radial segments increases, the iCOM CTF approaches that of the pixelated detector.
    • Similarly to pixelated iCOM, the CTF degrades quickly with increasing defocus. The effect is even more pronounced with large, few detector elements.
  • Since the CTF relies on the center of mass of detector segment jj, the outer collection angle of an annular detector should match the semi-convergence angle, α, for the COM approximation to be accurate.
    • An outer collection angle ≫qprobe\gg q_{\mathrm{probe}} results in over-estimation of the COM signal, and thus produces a CTF above unity.
  • This effect may be somewhat remedied by introducing radial rings which allows the detector to resolve the COM signal radially in addition to annularly.
  • For detectors with few annular segments, the 2D CTF is anisotropic, resulting in non-round atoms when convolved with the STO WPO.
  • The rotational-offset of the annular segments is reflected in the 2D CTF orientation.
    • Note this effect is obfuscated in the commonly-presented 1D radial averages.
  • Offsetting half of the ring’s segments by half of their annular span range (e.g. 45∘45^\circ for four segments spanning 90∘90^\circ each) further improves annular resolution, yielding a more isotropic CTF.
References
  1. Shibata, N., Findlay, S. D., Kohno, Y., Sawada, H., Kondo, Y., & Ikuhara, Y. (2012). Differential phase-contrast microscopy at atomic resolution. Nature Physics, 8(8), 611–615. 10.1038/nphys2337
  2. Lazić, I., & Bosch, E. G. T. (2017). Analytical Review of Direct Stem Imaging Techniques for Thin Samples. In Advances in Imaging and Electron Physics (pp. 75–184). Elsevier. 10.1016/bs.aiep.2017.01.006
Segmented Detector CTF
Segmented Detectors
Segmented Detector CTF
Segmented SSB
Elemental MicroscopyElemental Microscopy
Reviews & foundational concepts in microscopy-based imaging
Curvenote
Terms & Privacy