Evaluating the Transfer of Information in Phase Retrieval STEM Techniques

Julie Marie Bekkevold; Stephanie M Ribet; Mary C Scott; Lewys Jones; Colin Ophus; Georgios Varnavides

doi:10.69761/ehch7395

Computational Article

Contents

The direct ptychographic methods we have introduced so far retrieve the phase information directly from the interference between the direct and scattered beams. Still, the scattering redundancy contained in the observed diffraction intensities can be used to solve the inverse scattering problem, by iteratively obtaining self-consistent estimates for the sample and probe Rodenburg & Maiden, 2019. This leverages our understanding of the physics of the interaction between the probe and the sample, as well as the STEM Image Formation mechanism – collectively known as the “forward model”.

The flexibility of the ptychographic forward model allows us to reconstruct increasingly complex scattering physics and phenomena. Table 6.1 summarizes various scattering physics approximations and the corresponding ptychographic techniques used to reconstruct them. In what follows, we focus on the WPOA and thus use single-slice ptychography. Extending our analyses to mixed-state and multi-slice ptychography is left for future work.

Table 6.1:Incomplete summary of ptychographic techniques and their usecases.

Applicability/Physical Phenomenon	Conventional Name/Reference
Thin or weakly-scattering objects	Single-slice ptychography Maiden & Rodenburg, 2009
‘Thick’ or multiply-scattering objects	Multi-slice ptychography Chen et al., 2021
Partial probe coherence	Mixed-state ptychography Thibault & Menzel, 2013
Tilt-series of ‘thick’ objects	Joint ptychographic tomography Lee et al., 2023

Numerical White-Noise Object¶

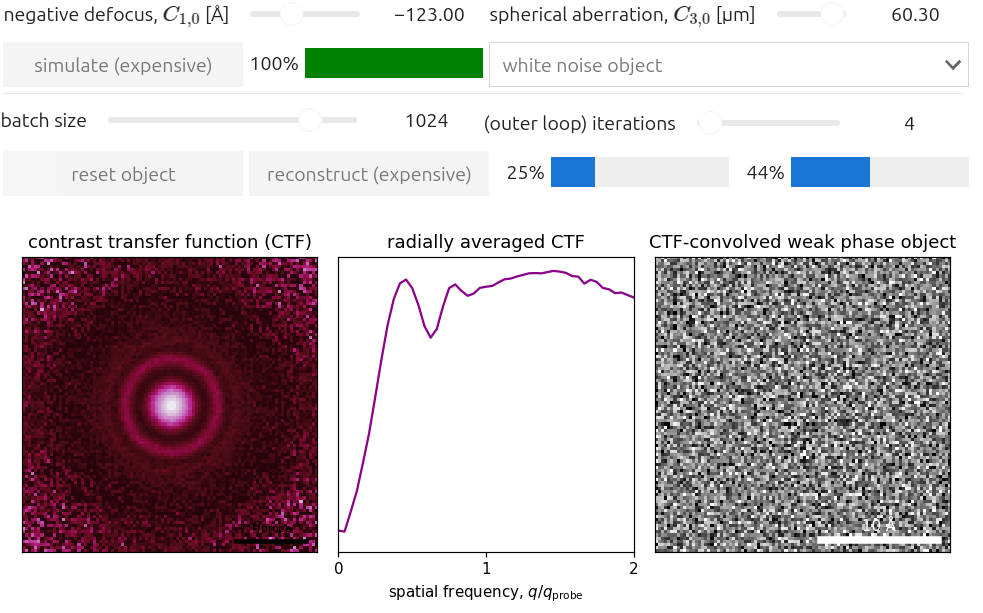
The iterative nature of iterative ptychography does not lend itself well to analytical CTF expressions like the ones derived in the previous sections. Instead, we use a numerical scheme to estimate the transfer of information using ptychographic reconstructions.

We isolate the dependence of the sample potential during phase-retrieval by reconstructing a White noise object, with scattering information across all spatial frequencies. Specifically, we define a 2D white noise sample in diffraction space using random phases drawn from a Normal distribution, and a constant unity amplitude:

\begin{aligned} \tilde{\phi}(\bm{q}) &\sim \mathcal{N}(0,1) \quad \forall \, \bm{q}, \quad \text{such that} \quad \tilde{\phi}(\bm{q}) = \tilde{\phi}^{\ast}(-\bm{q}), \\ \phi(\bm{r}) &= \mathcal{F}^{-1}_{\bm{q}\rightarrow \bm{r}}\left[\tilde{\phi}(\bm{q})\right] \\ \end{aligned},

(6.1)

where $\mathcal{N}(0,1)$ denotes a zero-mean normal distribution with unit standard deviation.

The white-noise object is then used to perform Nyquist-sampled STEM simulations using Equations (2.1) - (2.3). Following phase-retrieval on the simulated datasets, the magnitude of the CTF can be directly estimated using the power spectrum of the reconstructed phase, $\phi^{\prime}(\bm{r})$ :

\left|\mathcal{L}^{\mathrm{numerical}}(\bm{q}) \right| = \left| \mathcal{F}_{\bm{r} \rightarrow \bm{q}} \left[ \phi^{\prime}(\bm{r}) \right] \right|.

(6.2)

Iterative Ptychography CTF¶

Effect of various probe aberrations and iterations on the CTF for iterative ptychography with a pixelated detector.
The resulting CTF is shown on the left panel, with its radial average in the middle panel, and its effect on example weak phase objects on the right panel.
Note that the batch size refers to the number of probe positions which are simultaneously updated which impacts the convergence of the ptychographic reconstruction. — Figure 6.1:Effect of various probe aberrations and iterations on the CTF for iterative ptychography with a pixelated detector. The resulting CTF is shown on the left panel, with its radial average in the middle panel, and its effect on example weak phase objects on the right panel. Note that the batch size refers to the number of probe positions which are simultaneously updated which impacts the convergence of the ptychographic reconstruction.

While, in contrast to direct ptychographic techniques, iterative ptychography can recover both the sample and the probe through “blind deconvolution”, in practice, robust estimates of the aberration coefficients significantly improve the reconstruction quality and convergence. Figure 6.1 plots (6.2) for low-order isotropic aberration coefficients, namely $C_{1,0}$ and $C_{3,0}$ . We note the following:

At early iterations (and non-zero $C_{1,0}$ / $C_{3,0}$ ), the iterative ptychography CTF illustrates “Thon-like” oscillations Thon, 1966.
With more iterations, the CTF approaches the ideal unity CTF, with all spatial frequencies recovered exactly.
Lower-spatial frequencies are slower to converge.
The super-resolution capabilities of iterative ptychography, are hinted to by the non-zero corner regions of the 2D CTF.

References¶

Rodenburg, J., & Maiden, A. (2019). Ptychography. In Springer Handbook of Microscopy (pp. 819–904). Springer International Publishing. 10.1007/978-3-030-00069-1_17
Maiden, A. M., & Rodenburg, J. M. (2009). An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy, 109(10), 1256–1262. 10.1016/j.ultramic.2009.05.012
Chen, Z., Jiang, Y., Shao, Y.-T., Holtz, M. E., Odstrčil, M., Guizar-Sicairos, M., Hanke, I., Ganschow, S., Schlom, D. G., & Muller, D. A. (2021). Electron ptychography achieves atomic-resolution limits set by lattice vibrations. Science, 372(6544), 826–831. 10.1126/science.abg2533
Thibault, P., & Menzel, A. (2013). Reconstructing state mixtures from diffraction measurements. Nature, 494(7435), 68–71. 10.1038/nature11806
Lee, J., Lee, M., Park, Y., Ophus, C., & Yang, Y. (2023). Multislice Electron Tomography Using Four-Dimensional Scanning Transmission Electron Microscopy. Physical Review Applied, 19(5). 10.1103/physrevapplied.19.054062
Thon, F. (1966). Notizen: Zur Defokussierungsabhängigkeit des Phasenkontrastes bei der elektronenmikroskopischen Abbildung. Zeitschrift Für Naturforschung A, 21(4), 476–478. 10.1515/zna-1966-0417

Pixelated Detector CTF

Pixelated tcBF

Segmented Detector CTF

Segmented Detectors

[cite-Rodenburg_2019] Rodenburg, J., & Maiden, A. (2019). Ptychography. In Springer Handbook of Microscopy (pp. 819–904). Springer International Publishing. 10.1007/978-3-030-00069-1_17

[cite-Maiden_2009] Maiden, A. M., & Rodenburg, J. M. (2009). An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy, 109(10), 1256–1262. 10.1016/j.ultramic.2009.05.012

[cite-Chen_2021] Chen, Z., Jiang, Y., Shao, Y.-T., Holtz, M. E., Odstrčil, M., Guizar-Sicairos, M., Hanke, I., Ganschow, S., Schlom, D. G., & Muller, D. A. (2021). Electron ptychography achieves atomic-resolution limits set by lattice vibrations. Science, 372(6544), 826–831. 10.1126/science.abg2533

[cite-Thibault_2013] Thibault, P., & Menzel, A. (2013). Reconstructing state mixtures from diffraction measurements. Nature, 494(7435), 68–71. 10.1038/nature11806

[cite-Lee_2023] Lee, J., Lee, M., Park, Y., Ophus, C., & Yang, Y. (2023). Multislice Electron Tomography Using Four-Dimensional Scanning Transmission Electron Microscopy. Physical Review Applied, 19(5). 10.1103/physrevapplied.19.054062

[cite-Thon_1966] Thon, F. (1966). Notizen: Zur Defokussierungsabhängigkeit des Phasenkontrastes bei der elektronenmikroskopischen Abbildung. Zeitschrift Für Naturforschung A, 21(4), 476–478. 10.1515/zna-1966-0417

Iterative Ptychography with a Pixelated Detector

Numerical White-Noise Object¶

Iterative Ptychography CTF¶